NASA Electromagnetic Spectrum 04-07

The Electromagnetic Spectrum

As it was explained in the Introductory Article on the Electromagnetic Spectrum, electromagnetic radiation can be described as a stream of photons, each traveling in a wave-like pattern, carrying energy and moving at the speed of light. In that section, it was pointed out that the only difference betweenradio waves, visible light and gamma rays is the energy of the photons. Radio waves have photons with the lowest energies.Microwaves have a little more energy than radio waves.Infrared has still more, followed by visible, ultraviolet, X-raysand gamma rays.

The amount of energy a photon has can cause it to behave more like a wave, or more like a particle. This is called the "wave-particle duality" of light. It is important to understand that we are not talking about a difference in what light is, but in how it behaves. Low energy photons (such as radio photons) behave more like waves, while higher energy photons (such as X-rays) behave more like particles.

The electromagnetic spectrum can be expressed in terms of energy, wavelength or frequency. Each way of thinking about the EM spectrum is related to the others in a precise mathematical way. Scientists represent wavelength and frequency by the Greek letters lambda (λ) and nu (ν). Using those symbols, the relationships between energy, wavelength and frequency can be written as:

wavelength equals the speed of light divided by the frequency
or
λ = c / ν

and

energy equals Planck's constant times the frequency
or
E = h × ν

Where:

• λ is the wavelength
• ν is the frequency
• E is the energy
• c is the speed of light, c = 299,792,458 m/s (186,212 miles/second)
• h is Planck's constant, h = 6.626 x 10^-27 erg-seconds

Both the speed of light and Planck's constant are constant – they never change in value.

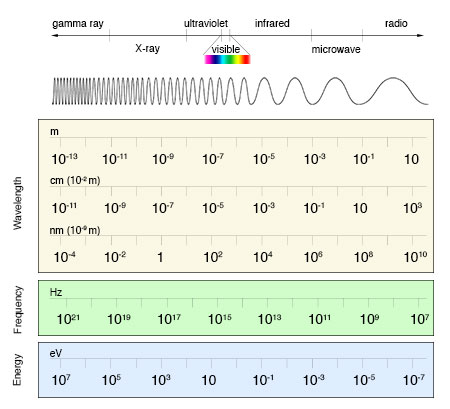
Conversion between wavelength, frequency and energy for the electromagnetic spectrum. (Click image for a larger version.)

Show a chart of the wavelength, frequency, and energy regimes of the spectrum

Astronomy Across the Electromagnetic Spectrum

While all light across the electromagnetic spectrum is fundamentally the same thing, the way that astronomersobserve light depends on the portion of the spectrum they wish to study.

For example, different detectors are senstive to different wavelenths of light. In addition, not all light can get through the Earth's atmosphere, so for some wavelengths we have to use telescopes aboard satellites. Even the way we collect the light can change depending on the wavelength. Astronomers must have a number of different telescopes and detectors to study the light from celestial objects across the electromagnetic spectrum.

A sample of telescopes (operating as of February 2013) operating at wavelengths across the electromagnetic spectrum. Several of these observatories observe more than one band of the EM spectrum, and those are placed within the band of their primary instrument(s).

The represented observatories are: HESS, Fermi and Swift for gamma-ray, NuSTAR and Chandra for X-ray, GALEX for ultraviolet, Kepler, Hubble, Keck (I and II), SALT, and Gemini (South) for visible, Spitzer, Herschel, and Sofia for infrared, Planck and CARMA for microwave, Spektr-R, Greenbank, and VLA for radio. Click here to see this image with the observatories labeled.